De bonnes bases en mathématiques : focus sur les représentations mentales des quantités

Vous avez des élèves qui utilisent encore leurs doigts pour des calculs simples après la 3e année? Qui ne s’aperçoivent pas du tout quand les réponses à leurs calculs n’ont vraiment pas de sens? Qui doivent compter les points sur les dés alors que les autres élèves de la classe n’ont plus besoin de le faire?

Pour s’assurer que nos jeunes élèves maîtrisent bien les préalables au développement des compétences numériques ou pour mieux comprendre la nature des difficultés persistantes en mathématiques chez plusieurs de nos élèves de 2e ou 3e cycle au primaire, pensons à observer leurs représentations mentales des quantités.

Les représentations mentales des quantités englobent trois composantes : le subitizing, l’estimation et la ligne numérique mentale.

Subitizing

Le subitizing est la perception précise et quasi instantanée de petites quantités. 

• Face à une collection de trois blocs ou quatre points sur un dé, il n’est pas nécessaire de compter ou de dénombrer pour identifier la quantité exacte. C’est un processus qui se développe d’abord de façon innée. Des scientifiques ont même réussi à démontrer la présence de cette perception chez les bébés et les animaux.

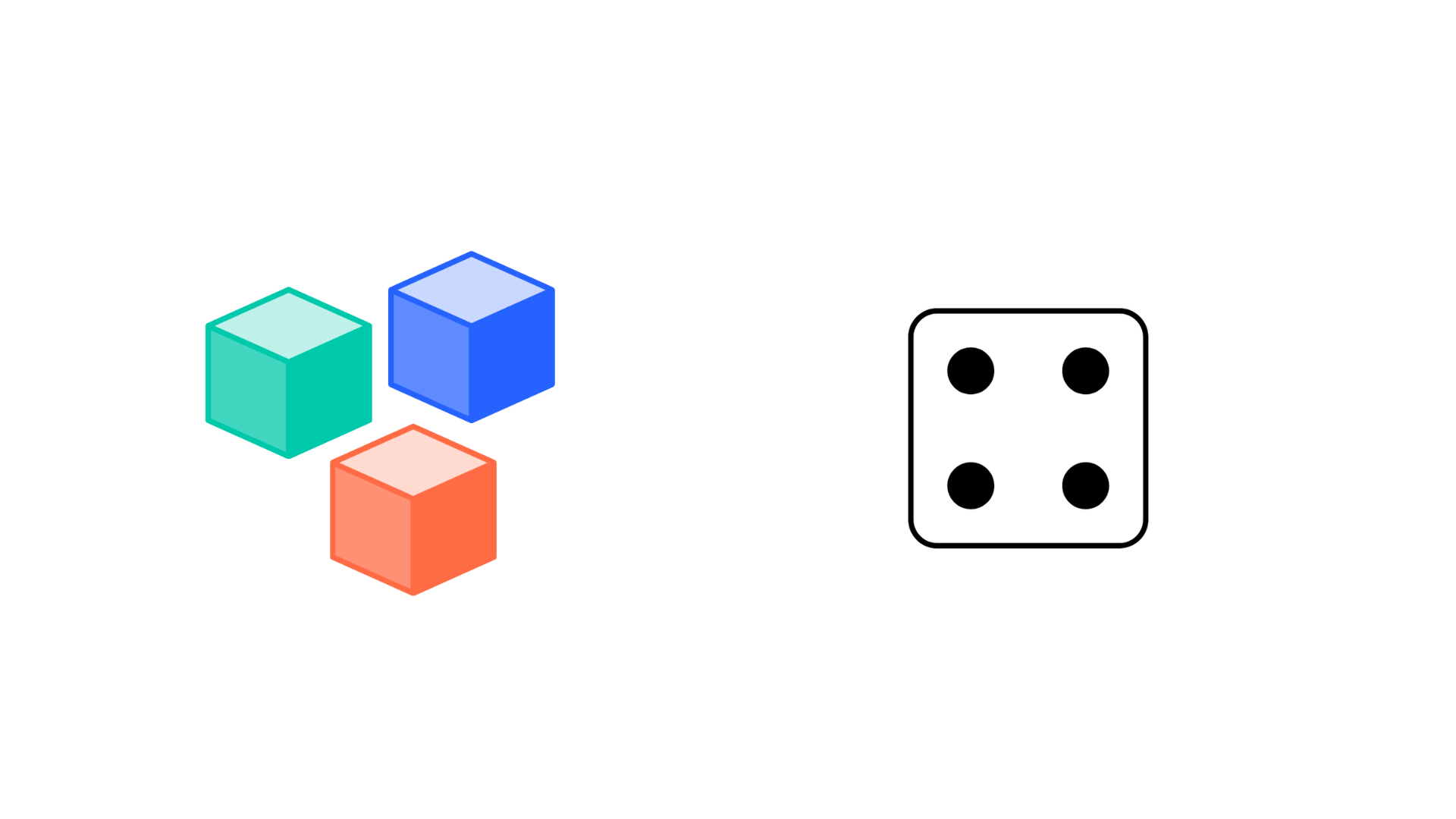
À l’école, on pousse cette perception un peu plus loin en apprenant à organiser les représentations des quantités et à reconnaître ces représentations. Cela nous permet de subitizer des quantités un peu plus grandes, comme dans les images ci-dessous. Nous n’avons pas besoin de compter ou de dénombrer pour identifier ces quantités, mais ce n’est pas acquis chez les élèves du préscolaire et des premières années du primaire. Le besoin de compter et d’être exposés à plusieurs reprises à ces représentations sera nécessaire avant d’apprendre à les reconnaître instantanément.

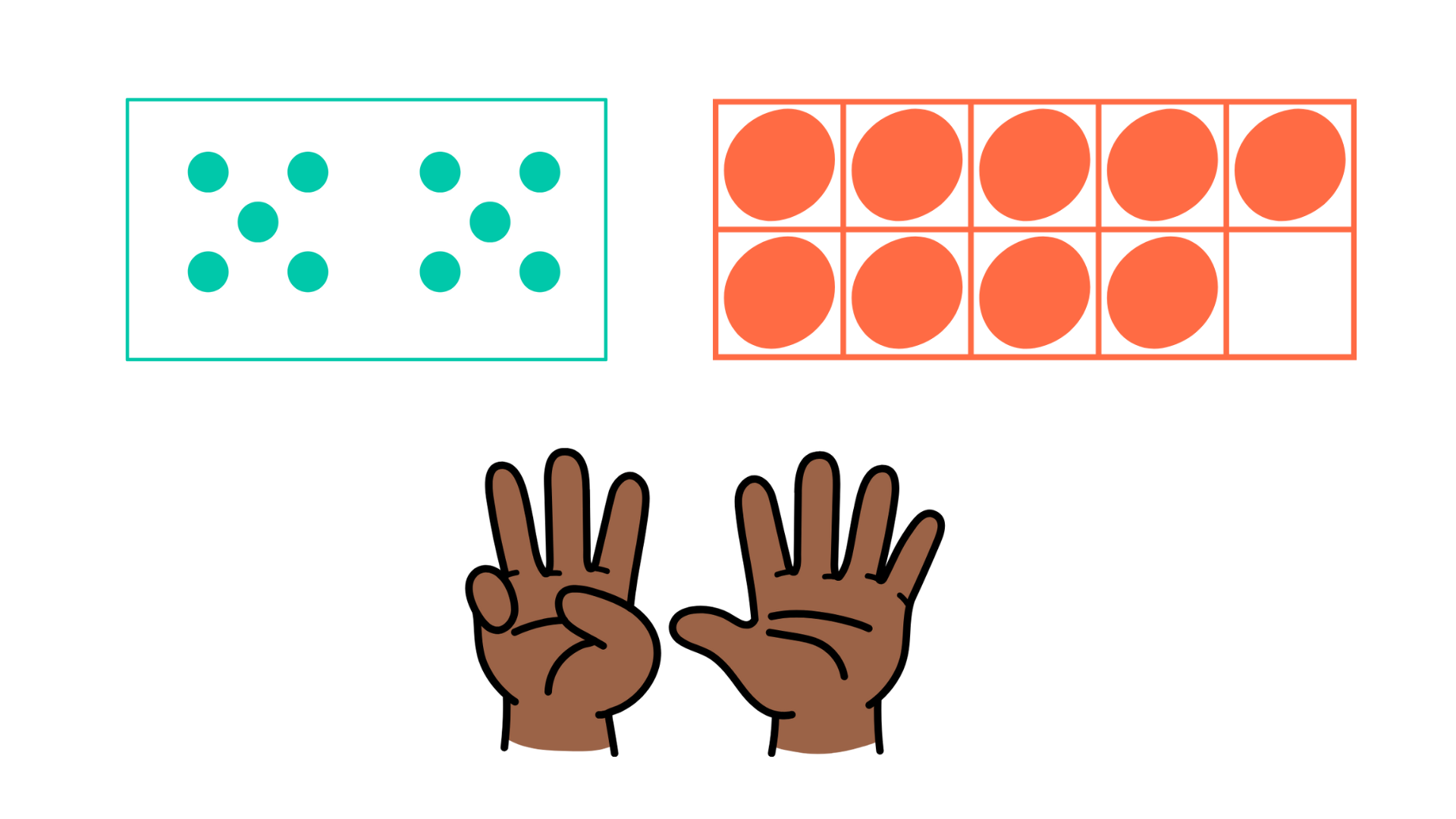
En classe, on peut le remarquer lorsque l'élève compte ses doigts. Si on lui demande de nous montrer « quatre » avec ses doigts et que l’élève compte ses doigts avant de nous montrer sa main avec quatre doigts en l’air, c’est un indice que ses habiletés de subitizing ne sont pas encore bien développées. Ce comportement normal chez les tout-petits ne l’est plus en vieillissant. 

Chez certaines personnes, cette perception tarde à se développer ou manque de précision et il est alors difficile, voire impossible, pour elles d’identifier précisément les petites quantités sans dénombrer. Quand les autres élèves de la classe n’ont plus besoin de dénombrer pour identifier les petites quantités, il peut être judicieux de consulter l’orthopédagogue de l’école pour les élèves qui ont encore besoin de le faire. Cela dit, on ne les empêche jamais d’utiliser leurs doigts pour calculer, les élèves cesseront de le faire dès que ça ne leur sera plus nécessaire.

Estimation

L’estimation est en quelque sorte le prolongement du subitizing à de plus grandes quantités. Il s’agit de la perception approximative et quasi instantanée de plus grandes quantités. 

• Il est possible d’estimer rapidement et assez précisément le nombre de points dans cette image, sans compter ni dénombrer. Toutefois, c’est beaucoup plus facile avec l’image des dix points organisés en deux groupes de cinq. La plupart des gens donneront un nombre très près de dix, sans pouvoir affirmer avec certitude qu’il y a exactement dix points.

  

• Plus la quantité est grande, moins notre estimation est précise et c’est normal. Dans cette image, la plupart des gens estimeront qu’il y a entre 70 et 110 points. Il faudra les compter pour savoir qu’il y en a 90. Vers l’âge de 11 ans, les capacités de subitizing et d’estimation sont typiquement semblables à celles des adultes.

Ligne numérique mentale

La ligne numérique mentale est une organisation mentale des quantités qui s’installe inconsciemment au fur et à mesure que l’on développe notre sens du nombre. Les quantités sont ordonnées sur une sorte de droite numérique très précise pour les petites quantités et de moins en moins précise pour les grandes quantités. Sans le savoir, nous nous référons à cette ligne numérique mentale pour ordonner et comparer les nombres entre eux. Cette organisation mentale est approximative chez les jeunes élèves et devient rapidement de plus en plus précise. Déjà avant l’âge de 8 ans, la ligne numérique mentale de l’enfant est précise pour les nombres de 0 à 100. Il y a une forte corrélation entre la ligne numérique mentale et les performances arithmétiques, mathématiques et de résolution de problèmes.

Avoir de bonnes habiletés en représentation mentale des quantités permet de traiter facilement les quantités et les nombres, de les ordonner, de les comparer et d’en faire une évaluation précise pour les petites quantités ou une estimation pour les grandes.

Cela joue notamment un rôle dans :

• les ancrages à cinq et à dix;

• le calcul mental précis;

• le calcul mental approximatif;

• l’estimation du temps;

• etc.

L’élève qui est capable d’utiliser facilement et efficacement ses doigts pour calculer aura une longueur d’avance sur l’élève qui doit d’abord compter ses doigts à chaque fois. Lorsque viendra le moment de passer aux représentations semi-concrètes et de représenter les quantités par des dessins, l’élève avec une bonne représentation mentale des quantités pourra repérer facilement les erreurs d’inattention dans ses dessins. L’élève avec des représentations solides des quantités aura aussi plus de facilité à comprendre les fractions et pourra se les représenter mentalement comme une partie d’un tout ou comme une partie d’une collection, selon ce qui est le plus approprié à la situation.

Les représentations mentales des quantités aident aussi à visualiser les problèmes mathématiques et à se représenter les quantités en contexte. 

• Prenons un problème où l’on propose d’acheter un huitième de melon d’eau par élève pour le diner de classe de fin d’année, sachant qu’il y a 25 élèves dans la classe. L’élève qui a une bonne représentation mentale des quantités pourra visualiser le problème de différentes façons et se mettre à douter de ses calculs après avoir obtenu 31 melons à acheter. Le doute s’installera d’abord parce que 31 melons pour 25 personnes, c’est beaucoup, mais aussi parce qu’au fil du problème, l’élève l’aura visualisé de différentes façons et aura été en mesure de vérifier ses calculs en faisant des approximations dans sa tête.

Soulignons l’importance de proposer aux élèves des problèmes mathématiques qui ont du sens, de façon à ce que les jeunes qui ont des représentations mentales justes et qui tentent de se représenter les problèmes en contexte puissent s’appuyer sur ces représentations pour construire du sens autour des concepts mathématiques utilisés. Si on avait proposé d’acheter huit melons d’eau par jeune, la représentation en contexte d’un diner de fin d’année avec 200 melons d’eau pour 25 élèves aurait semblé irréaliste et l’élève aurait pu croire à une erreur dans ses calculs, même si cette réponse est juste selon les données du problème.

Plusieurs recherches ont montré une forte corrélation entre les habiletés de représentation mentale des quantités et les performances futures des élèves en mathématiques. Nous savons aussi qu’il y a des liens entre certaines difficultés en mathématiques et de faibles habiletés en représentation mentale des quantités, notamment chez des élèves qui ont des difficultés à dénombrer, à mémoriser les faits arithmétiques, à réaliser des calculs mentaux simples ou à faire du calcul écrit.

Il y a de plus en plus de recherches qui présentent des interventions efficaces portant sur le développement des habiletés de représentations mentales des quantités. Il y a même des scientifiques qui ont développé des programmes d’intervention pour la classe. De plus en plus d’orthopédagogues et d’orthophonistes sont formés pour intervenir en mathématiques et soutenir les élèves qui présentent des difficultés avec les représentations mentales des quantités, en collaboration avec les enseignants.

Les élèves qui ont de faibles habiletés en représentation des quantités ont souvent une mauvaise perception du temps. Utiliser un time-timer leur permet d’associer une représentation visuelle à une quantité de temps et de rendre cette notion plus concrète.

On ne peut jamais assez recommander l’utilisation fréquente du matériel de manipulation en mathématiques et des représentations tout au long du primaire. Ces outils sont essentiels pour aider les élèves à développer des compétences solides en mathématiques.

Un peu plus sur l'autrice

Orthopédagogue, Kim est également formatrice et autrice en éducation. Lors de ses études à la maîtrise, elle s’est intéressée aux difficultés persistantes en mathématiques et s’est jointe à l’équipe de recherche du Laboratoire sur l’enseignement et l’apprentissage des mathématiques de l’Université Concordia avec qui elle collabore toujours. Kim croit profondément que l’établissement de liens entre la recherche et la pratique est ce qui fera de nous de meilleurs pédagogues et ce qui permettra à plus d’enfants, avec ou sans difficulté d’apprentissage, de vivre un parcours scolaire épanouissant.